
 Прямая касается окружности в точке K. Центр окружности – точка O. Хорда KM образует с касательной угол, равный 40°. Найдите величину угла KOM. Ответ дайте в градусах.
Прямая касается окружности в точке K. Центр окружности – точка O. Хорда KM образует с касательной угол, равный 40°. Найдите величину угла KOM. Ответ дайте в градусах.
OK перпендикулярен к
касательной (по
свойству касательной), т.е. угол между OK и
касательной равен 90°.
Следовательно, /OKM=90°-40°=50°
Треугольник OMK -
равнобедренный (т.к. OM и OK - радиусы окружности и, соответственно, равны друг другу).
По
свойству равнобедренного треугольника /OKM=/OMK=50°
/OKM+/OMK+/KOM=180° (по
теореме о сумме углов треугольника)
50°+50°+/KOM=180°
/KOM=80°
Ответ: /KOM=80°
Поделитесь решением
Присоединяйтесь к нам...
 В треугольнике АВС углы А и С равны 20° и 50° соответственно. Найдите угол между высотой ВН и биссектрисой BD.
В треугольнике АВС углы А и С равны 20° и 50° соответственно. Найдите угол между высотой ВН и биссектрисой BD.
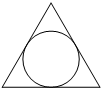 Сторона равностороннего треугольника равна 2√
Сторона равностороннего треугольника равна 2√
 Точка O – центр окружности, на которой лежат точки S, T и V таким образом, что OSTV – ромб. Найдите угол OVT. Ответ дайте в градусах.
Точка O – центр окружности, на которой лежат точки S, T и V таким образом, что OSTV – ромб. Найдите угол OVT. Ответ дайте в градусах.
 Катеты прямоугольного треугольника равны 8 и 6. Найдите синус наименьшего угла этого треугольника.
Катеты прямоугольного треугольника равны 8 и 6. Найдите синус наименьшего угла этого треугольника.
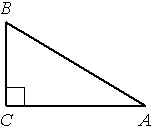 В треугольнике ABC угол C прямой, BC=4, sinA=0,8. Найдите AB.
В треугольнике ABC угол C прямой, BC=4, sinA=0,8. Найдите AB.
Комментарии:
(2017-12-17 21:41:43) Администратор: Мы не помогаем решить домашнее задание, цель сайта - подробно разобрать задачи, которые будут на экзаменах, чтобы учащиеся научились их решать самостоятельно. Если найдете похожую задачу на сайте fipi.ru, отправьте заявку на добавление задачи, и мы ее обязательно добавим.
(2017-12-07 20:21:01) : . Катеты прямоугольного треугольника равны 20 41 и 25 41 . Найдите высоту, проведённую к гипотенузе.