
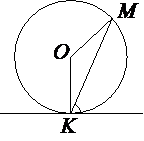 Прямая касается окружности в точке K. Точка O – центр окружности. Хорда KM образует с касательной угол, равный 83°. Найдите величину угла OMK. Ответ дайте в градусах.
Прямая касается окружности в точке K. Точка O – центр окружности. Хорда KM образует с касательной угол, равный 83°. Найдите величину угла OMK. Ответ дайте в градусах.
OK перпендикулярен к
касательной (по
свойству касательной), т.е. угол между OK и
касательной равен 90°.
Следовательно, /OKM=90°-83°=7°
Треугольник OMK -
равнобедренный (т.к. OM и OK - радиусы окружности и, соответственно, равны друг другу).
По
свойству равнобедренного треугольника /OKM=/OMK=7°
Ответ: /OMK=7°
Поделитесь решением
Присоединяйтесь к нам...
 Площадь равнобедренного треугольника равна 196√
Площадь равнобедренного треугольника равна 196√
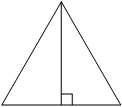 Высота равностороннего треугольника равна 13√3. Найдите сторону этого треугольника.
Высота равностороннего треугольника равна 13√3. Найдите сторону этого треугольника.
 Окружность, вписанная в треугольник ABC, касается его сторон в точках M, K и P. Найдите углы треугольника ABC, если углы треугольника MKP равны 62°, 54° и 64°.
Окружность, вписанная в треугольник ABC, касается его сторон в точках M, K и P. Найдите углы треугольника ABC, если углы треугольника MKP равны 62°, 54° и 64°.
 Отрезки AB и CD являются хордами окружности. Найдите расстояние от центра окружности до хорды CD, если AB=20, CD=48, а расстояние от центра окружности до хорды AB равно 24.
Отрезки AB и CD являются хордами окружности. Найдите расстояние от центра окружности до хорды CD, если AB=20, CD=48, а расстояние от центра окружности до хорды AB равно 24.
 На отрезке AB выбрана точка C так, что AC=12 и BC=3. Построена окружность с центром A, проходящая через C. Найдите длину отрезка касательной, проведённой из точки B к этой окружности.
На отрезке AB выбрана точка C так, что AC=12 и BC=3. Построена окружность с центром A, проходящая через C. Найдите длину отрезка касательной, проведённой из точки B к этой окружности.
Комментарии:
(2016-10-23 22:30:42) Администратор: Ольга, Мы не помогаем решить домашнее задание, цель сайта - подробно разобрать задачи, которые будут на экзаменах, чтобы учащиеся научились их решать самостоятельно. Если найдете похожую задачу на сайте fipi.ru, пишите, обязательно добавим.
(2016-10-23 09:55:01) Ольга: На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠NBA=73°. Найдите угол NMB. Ответ дайте в градусах.
(2014-05-29 14:12:22) Администратор: Спасибо, номер изменен.
(2014-05-29 14:09:54) : у задачи новый номер - 0BF928