
 В трапеции ABCD AD=8, BC=5, а её площадь равна 13. Найдите площадь треугольника ABC.
В трапеции ABCD AD=8, BC=5, а её площадь равна 13. Найдите площадь треугольника ABC.
Площадь
трапеции равна h*(a+b)/2, где a и b - основания трапеции, h - высота трапеции.
hтрапеции*(8+5)/2=13 (по условию задачи)
h=13/6,5=2
 Проведем
высоту треугольника ABC, как показано на рисунке.
Проведем
высоту треугольника ABC, как показано на рисунке.
hтреугольника=hтрапеции, так как они обе перпендикулярны одним и тем же параллельным основаниям трапеции и образуют прямоугольник.
Sтреугольника=hтреугольника*BC/2=2*5/2=5
Ответ: Sтреугольника=5
Поделитесь решением
Присоединяйтесь к нам...
 На отрезке AB выбрана точка C так, что AC=12 и BC=3. Построена окружность с центром A, проходящая через C. Найдите длину отрезка касательной, проведённой из точки B к этой окружности.
На отрезке AB выбрана точка C так, что AC=12 и BC=3. Построена окружность с центром A, проходящая через C. Найдите длину отрезка касательной, проведённой из точки B к этой окружности.
 Проектор полностью освещает экран A высотой 80 см, расположенный на расстоянии 250 см от проектора. На каком наименьшем расстоянии
(в сантиметрах) от проектора нужно расположить экран B высотой 160 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными?
Проектор полностью освещает экран A высотой 80 см, расположенный на расстоянии 250 см от проектора. На каком наименьшем расстоянии
(в сантиметрах) от проектора нужно расположить экран B высотой 160 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными?
 Картинка имеет форму прямоугольника со сторонами 24 см и 37 см. Её наклеили на белую бумагу так, что вокруг картинки получилась белая окантовка одинаковой ширины. Площадь, которую занимает картинка с окантовкой, равна 1440 см2. Какова ширина окантовки? Ответ дайте в сантиметрах.
Картинка имеет форму прямоугольника со сторонами 24 см и 37 см. Её наклеили на белую бумагу так, что вокруг картинки получилась белая окантовка одинаковой ширины. Площадь, которую занимает картинка с окантовкой, равна 1440 см2. Какова ширина окантовки? Ответ дайте в сантиметрах.
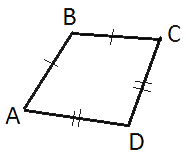 В выпуклом четырехугольнике ABCD AB=BC, AD=CD, ∠B=100° , ∠D=104°. Найдите угол A . Ответ дайте в градусах.
В выпуклом четырехугольнике ABCD AB=BC, AD=CD, ∠B=100° , ∠D=104°. Найдите угол A . Ответ дайте в градусах.
Какое из следующих утверждений верно?
1) Все углы ромба равны.
2) Если стороны одного четырёхугольника соответственно равны сторонам другого четырёхугольника, то такие четырёхугольники равны.
3) Через любую точку, лежащую вне окружности, можно провести две касательные к этой окружности.
Комментарии:
(2015-12-24 19:18:01) флюра: спасибо. очень удобно.