
 Высота BH ромба ABCD делит его сторону AD на отрезки AH=21 и HD=8. Найдите площадь ромба.
Высота BH ромба ABCD делит его сторону AD на отрезки AH=21 и HD=8. Найдите площадь ромба.
Площадь
ромба равна S=ah, где a - сторона ромба, h - высота ромба.
AD=AH+HD=21+8=29.
AD=AB=BC=CD (по
определению ромба).
Рассмотрим треугольник ABH.
ABH -
прямоугольный (т.к. BH -
высота), тогда по
теореме Пифагора: AB2=BH2+AH2
292=BH2+212
841=BH2+441
BH2=400
BH=20
Sромба=AD*BH=29*20=580
Ответ: Sромба=580
Поделитесь решением
Присоединяйтесь к нам...
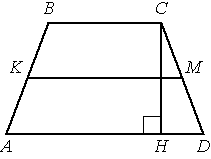 В трапеции АВСD боковые стороны AB и CD равны, СН — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 10, а меньшее основание BC равно 4.
В трапеции АВСD боковые стороны AB и CD равны, СН — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 10, а меньшее основание BC равно 4.
 Радиус окружности, описанной около квадрата, равен 38√2. Найдите радиус окружности, вписанной в этот квадрат.
Радиус окружности, описанной около квадрата, равен 38√2. Найдите радиус окружности, вписанной в этот квадрат.
 В треугольнике ABC угол C равен 90°, sinB=5/17, AB=51. Найдите AC.
В треугольнике ABC угол C равен 90°, sinB=5/17, AB=51. Найдите AC.
 Радиус вписанной в квадрат окружности равен 14√
Радиус вписанной в квадрат окружности равен 14√
 Найдите площадь параллелограмма, изображённого на рисунке.
Найдите площадь параллелограмма, изображённого на рисунке.
Комментарии: