
Какие из следующих утверждений верны?
1) Один из двух смежных углов острый, а другой тупой.
2) Площадь квадрата равна произведению двух его смежных сторон.
3) Все хорды одной окружности равны между собой.
Рассмотрим каждое утверждение:
1) "Один из двух
смежных углов острый, а другой тупой".
Острый угол - градусная мера от 0 до 90 градусов.
Прямой угол - градусная мера 90 градусов.
Тупой угол - градусная мера больше 90 градусов.
Так как сумма смежных углов равна 180°, то очевидно: если один из смежных углов больше 90°, то второй угол меньше 90°. Но если один из углов прямой (т.е. не острый и не тупой), то смежный ему угол тоже прямой. Следовательно, это утверждение неверно.
2) "Площадь
квадрата равна произведению двух его смежных сторон", это утверждение верно. Думаю, комментариев не требуется.
3) "Все хорды одной окружности равны между собой". Если рассмотреть первое свойство хорды, то становится понятно, что длина хорды зависит от ее удаленности от центра окружности, при чем диаметр - самая большая хорда. Поэтому это утверждение неверно.
Поделитесь решением
Присоединяйтесь к нам...
Какие из данных утверждений верны? Запишите их номера.
1) Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы равны 90°, то эти две прямые параллельны.
2) В любой четырёхугольник можно вписать окружность.
3) Центром окружности, описанной около треугольника, является точка пересечения серединных перпендикуляров к сторонам треугольника.
 Площадь прямоугольного треугольника равна 800√
Площадь прямоугольного треугольника равна 800√
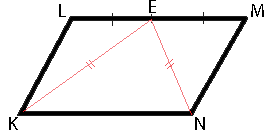 В параллелограмме KLMN точка E — середина стороны LM. Известно, что EK=EN. Докажите, что данный параллелограмм — прямоугольник.
В параллелограмме KLMN точка E — середина стороны LM. Известно, что EK=EN. Докажите, что данный параллелограмм — прямоугольник.
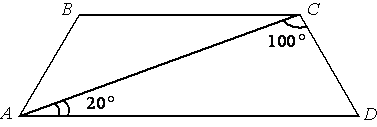 Найдите угол АВС равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной CD углы, равные 20° и 100° соответственно.
Найдите угол АВС равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной CD углы, равные 20° и 100° соответственно.
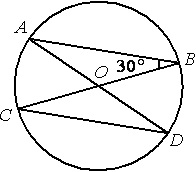 В окружности с центром в точке О проведены диаметры AD и BC, угол
ABO равен 30°. Найдите величину угла ODC.
В окружности с центром в точке О проведены диаметры AD и BC, угол
ABO равен 30°. Найдите величину угла ODC.
Комментарии: