
Какие из следующих утверждений верны?
1) Один из двух смежных углов острый, а другой тупой.
2) Площадь квадрата равна произведению двух его смежных сторон.
3) Все хорды одной окружности равны между собой.
Рассмотрим каждое утверждение:
1) "Один из двух
смежных углов острый, а другой тупой".
Острый угол - градусная мера от 0 до 90 градусов.
Прямой угол - градусная мера 90 градусов.
Тупой угол - градусная мера больше 90 градусов.
Так как сумма смежных углов равна 180°, то очевидно: если один из смежных углов больше 90°, то второй угол меньше 90°. Но если один из углов прямой (т.е. не острый и не тупой), то смежный ему угол тоже прямой. Следовательно, это утверждение неверно.
2) "Площадь
квадрата равна произведению двух его смежных сторон", это утверждение верно. Думаю, комментариев не требуется.
3) "Все хорды одной окружности равны между собой". Если рассмотреть первое свойство хорды, то становится понятно, что длина хорды зависит от ее удаленности от центра окружности, при чем диаметр - самая большая хорда. Поэтому это утверждение неверно.
Поделитесь решением
Присоединяйтесь к нам...
 Площадь параллелограмма ABCD равна 5. Точка E – середина стороны AD. Найдите площадь трапеции AECB.
Площадь параллелограмма ABCD равна 5. Точка E – середина стороны AD. Найдите площадь трапеции AECB.
 Сторона ромба равна 32, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
Сторона ромба равна 32, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
 Медиана BM и биссектриса AP треугольника ABC пересекаются в точке K, длина стороны AC относится к длине стороны AB как 6:5. Найдите отношение площади треугольника AKM к площади четырёхугольника KPCM.
Медиана BM и биссектриса AP треугольника ABC пересекаются в точке K, длина стороны AC относится к длине стороны AB как 6:5. Найдите отношение площади треугольника AKM к площади четырёхугольника KPCM.
 Биссектриса угла A параллелограмма ABCD пересекает сторону BC
в точке K. Найдите периметр параллелограмма, если BK=5, CK=14.
Биссектриса угла A параллелограмма ABCD пересекает сторону BC
в точке K. Найдите периметр параллелограмма, если BK=5, CK=14.
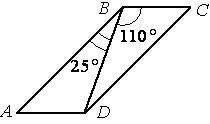 Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные
25° и 110°. Найдите меньший угол параллелограмма.
Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные
25° и 110°. Найдите меньший угол параллелограмма.
Комментарии: