
 В трапеции
ABCD AB=CD, /BDA=67° и /BDC=28°. Найдите угол ABD. Ответ дайте в градусах.
В трапеции
ABCD AB=CD, /BDA=67° и /BDC=28°. Найдите угол ABD. Ответ дайте в градусах.
Обратите внимание, рисунок не соответствует условию задачи (углы на рисунке заведомо меньше, чем в условии).
/ADC=/BDA+/BDC=67°+28°=95°.
Трапеция ABCD -
равнобедренная (т.к. AB=CD), следовательно, по
свойству равнобедренной трапеции, /BAD=/ADC=95°.
Сумма углов любого выпуклого n-угольника равна 180°*(n-2).
Тогда сумма углов трапеции равна 180°*(4-2)=360°, следовательно /ABC+/BCD=360°-95°-95°=170°
По тому же
свойству равнобедренной трапеции /ABC=/BCD, тогда каждый из этих углов равен 170°/2=85°
В любой трапеции основания параллельны (по
определению), т.е. AD||BC, тогда, рассматривая BD как секущую, заметим, что /CBD=/BDA=67° (т.к. это
внутренние накрест лежащие углы).
Тогда /ABD=/ABC-/CBD=85°-67°=18°
Ответ: /ABD=18°
Поделитесь решением
Присоединяйтесь к нам...
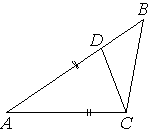 Точка D на стороне AB треугольника ABC выбрана так, что AD=AC. Известно, что ∠CAB=54° и ∠ACB=104°. Найдите угол DCB. Ответ дайте в градусах.
Точка D на стороне AB треугольника ABC выбрана так, что AD=AC. Известно, что ∠CAB=54° и ∠ACB=104°. Найдите угол DCB. Ответ дайте в градусах.
Сколько досок длиной 3,5 м, шириной 20 см и толщиной 10 мм выйдет из бруса длиной 140 дм, имеющего в сечении прямоугольник размером 50 см × 60 см?
 Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 15. Найдите BC, если AC=24.
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 15. Найдите BC, если AC=24.
 Основания трапеции равны 5 и 40, одна из боковых сторон равна 14, а косинус угла между ней и одним из оснований равен 3/5. Найдите площадь трапеции.
Основания трапеции равны 5 и 40, одна из боковых сторон равна 14, а косинус угла между ней и одним из оснований равен 3/5. Найдите площадь трапеции.
Косинус острого угла A треугольника ABC равен 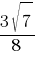 . Найдите sinA.
. Найдите sinA.
Комментарии: