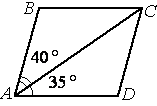Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 40° и 35°. Найдите больший угол параллелограмма.
По
свойству
параллелограмма /A=/C=35°+40°=75° и /B=/D.
Найдем углы B и D.
Стороны AD и BC параллельны (по
определению параллелограмма). Если рассмотреть AC как секущую к этим параллельным прямым, то становится очевидным, что /DAC=/BCA=35° (т.к. они
накрест лежащие).
Рассмотрим треугольник ABC.
По
теореме о сумме углов треугольника мы можем написать: 180°=/CAB+/B+/BCA
180°=40°+/B+35°
/B=105°=/D
105>75, следовательно углы B и D - бОльшие.
Ответ: больший угол равен 105°.
Поделитесь решением
Присоединяйтесь к нам...
Углы при одном из оснований трапеции равны 50° и 40°, а отрезки, соединяющие середины противоположных сторон трапеции, равны 15 и 13. Найдите основания трапеции.
Какие из данных утверждений верны? Запишите их номера.
1) На плоскости существует единственная точка, равноудалённая от концов отрезка.
2) В любой треугольник можно вписать окружность.
3) Если в параллелограмме две смежные стороны равны, то такой параллелограмм является ромбом.
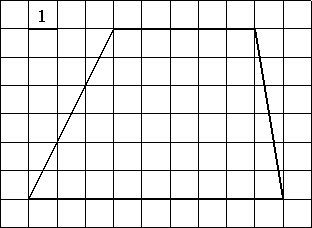Найдите площадь трапеции, изображённой на рисунке.
На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что
∠NBA=47°. Найдите угол NMB. Ответ дайте в градусах.
Укажите номера верных утверждений.
1) Центр описанной окружности равнобедренного треугольника лежит на высоте, проведённой к основанию треугольника.
2) Квадрат является прямоугольником.
3) Сумма углов любого треугольника равна
180°.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: