ОГЭ, Математика.
Геометрия: Задача №F48418
| Задача №312 из 1087
Условие задачи: | |
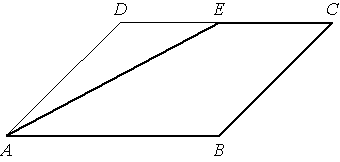 Площадь параллелограмма
ABCD равна 56. Точка E — середина стороны
CD. Найдите площадь трапеции AECB.
Площадь параллелограмма
ABCD равна 56. Точка E — середина стороны
CD. Найдите площадь трапеции AECB.
Решение задачи:
Первый вариант решения
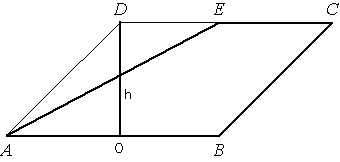
Проведем высоту
параллелограмма DO, как показано на рисунке. Площадь параллелограмма равна произведению стороны на высоту
параллелограмма.
S
параллелограмма=AB*h=56
А площадь
трапеции равна произведению полусуммы оснований на высоту.
S
трапеции=h*(AB+EC)/2.
EC=DC/2 (по условию задачи).
DC=AB (по
свойству параллелограмма).
Следовательно EC=AB/2.
Тогда S
трапеции=h*(AB+AB/2)/2 = h*(3*AB/2)/2 = h*3*AB/4=h*AB*3/4 = S
парал-ма*3/4=56*3/4=42.
Ответ: S
трапеции=42.
Второй вариант решения задачи
Прислал пользователь Юлия
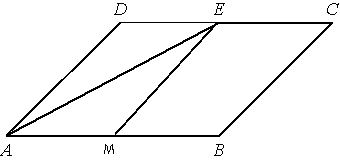
1) Отметим точку М на АB, так чтобы AM=MB
S
ADEM=S
MECB, т.к. ЕМ делит ABCD на равные части.
2) Треугольник AED равен треугольнику EAM (по
первому признаку):
/AED =
/EAM (т.к. AB||CD, AE - секущая, а эти углы -
внутренние накрест лежащие)
DЕ=AM
AE - общая сторона
3) Пусть площадь треугольника AED = х, тогда S
ABCD = 4x т.к EM делит ABCD пополам.
4x = 56
x = 14
4) S
AECB = S
ABCD - S
AED = 4x-x = 3x
S
AECB = 3*14 = 42
Ответ: площадь трапеции 42 см в кв.
Вы можете поблагодарить автора, написать свои претензии или предложения на
странице 'Про нас'
Другие задачи из этого раздела
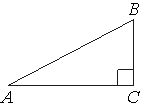 В треугольнике ABC угол C равен 90°, AC=4, AB=5. Найдите sinB.
В треугольнике ABC угол C равен 90°, AC=4, AB=5. Найдите sinB.
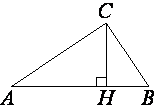 В прямоугольном треугольнике
ABC катет AC=8, а высота CH, опущенная на гипотенузу, равна 2√15. Найдите sin∠ABC.
В прямоугольном треугольнике
ABC катет AC=8, а высота CH, опущенная на гипотенузу, равна 2√15. Найдите sin∠ABC.
 Из вершины прямого угла C треугольника ABC проведена высота CP. Радиус окружности, вписанной в треугольник BCP, равен 60, тангенс угла BAC равен 5/12. Найдите радиус окружности, вписанной в треугольник ABC.
Из вершины прямого угла C треугольника ABC проведена высота CP. Радиус окружности, вписанной в треугольник BCP, равен 60, тангенс угла BAC равен 5/12. Найдите радиус окружности, вписанной в треугольник ABC.
 Докажите, что медиана треугольника делит его на два треугольника, площади которых равны между собой.
Докажите, что медиана треугольника делит его на два треугольника, площади которых равны между собой.
 В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 208. Найдите стороны треугольника ABC.
В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 208. Найдите стороны треугольника ABC.

 Площадь параллелограмма
ABCD равна 56. Точка E — середина стороны
CD. Найдите площадь трапеции AECB.
Площадь параллелограмма
ABCD равна 56. Точка E — середина стороны
CD. Найдите площадь трапеции AECB. Проведем высоту
параллелограмма DO, как показано на рисунке. Площадь параллелограмма равна произведению стороны на высоту
параллелограмма.
Проведем высоту
параллелограмма DO, как показано на рисунке. Площадь параллелограмма равна произведению стороны на высоту
параллелограмма. 1) Отметим точку М на АB, так чтобы AM=MB
1) Отметим точку М на АB, так чтобы AM=MB В треугольнике ABC угол C равен 90°, AC=4, AB=5. Найдите sinB.
В треугольнике ABC угол C равен 90°, AC=4, AB=5. Найдите sinB. В прямоугольном треугольнике
ABC катет AC=8, а высота CH, опущенная на гипотенузу, равна 2√
В прямоугольном треугольнике
ABC катет AC=8, а высота CH, опущенная на гипотенузу, равна 2√ Из вершины прямого угла C треугольника ABC проведена высота CP. Радиус окружности, вписанной в треугольник BCP, равен 60, тангенс угла BAC равен 5/12. Найдите радиус окружности, вписанной в треугольник ABC.
Из вершины прямого угла C треугольника ABC проведена высота CP. Радиус окружности, вписанной в треугольник BCP, равен 60, тангенс угла BAC равен 5/12. Найдите радиус окружности, вписанной в треугольник ABC. Докажите, что медиана треугольника делит его на два треугольника, площади которых равны между собой.
Докажите, что медиана треугольника делит его на два треугольника, площади которых равны между собой. В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 208. Найдите стороны треугольника ABC.
В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 208. Найдите стороны треугольника ABC.
Комментарии: