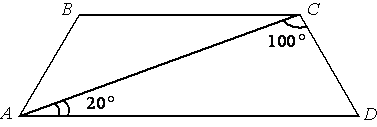
Найдите угол АВС равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной CD углы, равные 20° и 100° соответственно.
AD||BC (по
определению трапеции). Тогда AC является секущей для этих параллельных отрезков.
/BCA=/CAD, т.к. они
внутренние накрест-лежащие.
Тогда /BCD=20°+100°=120°.
По
свойству
равнобедренной трапеции /ABC=/BCD=120°.
Ответ: /ABC=120°.
Поделитесь решением
Присоединяйтесь к нам...
Точка крепления троса, удерживающего флагшток в вертикальном положении, находится на высоте 8 м от земли. Расстояние от основания флагштока до места крепления троса на земле равно 6 м. Найдите длину троса.
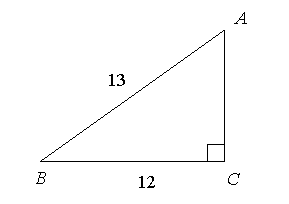Найдите площадь треугольника, изображённого на рисунке.
Найдите угол ABC . Ответ дайте в градусах.
В треугольнике ABC угол C равен 90°, sinA=8/9, AC=2√
Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите AC, если диаметр окружности равен 8,4, а AB=4.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: