
 Из вершины прямого угла C треугольника ABC проведена высота CP. Радиус окружности, вписанной в треугольник BCP, равен 5 см, тангенс угла ABC равен 2,4. Найдите радиус вписанной окружности треугольника ABC.
Из вершины прямого угла C треугольника ABC проведена высота CP. Радиус окружности, вписанной в треугольник BCP, равен 5 см, тангенс угла ABC равен 2,4. Найдите радиус вписанной окружности треугольника ABC.
Радиус вписанной окружности можно вычислить по формуле R=(AC+CB-AB)/2. Для этого необходимо вычислить длины всех сторон данного треугольника.
Рассмотрим треугольник ABC.
По
определению tgABC=AC/CB=2,4 => AC=2,4*CB.
По
теореме Пифагора AB2=AC2+CB2
AB2=(2,4*CB)2+CB2
AB2=(CB/2,4)2+(2,4*CB/2,4)2
AB2=5,76*CB2+CB2
AB2=6,76*CB2
AB=2,6*CB
Необходимо вычислить CB.
Рассмотрим треугольник BCP.
По
определению tgABC=CP/BP=2,4 => CP=2,4*BP
По
теореме Пифагора CB2=CP2+BP2
CB2=(2,4*BP)2+BP2
CB2=6,76*BP2
CB=2,6*BP
BP=CB/2,6
r=(BP+CP-CB)/2
2*r=BP+2,4*BP-2,6*BP
2*5=0,8*BP
BP=12,5
CB=2,6*BP=2,6*12,5=32,5
Вычислив CB, мы можем вычислить AB и AC, указанные выше:
AB=2,6*CB=2,6*32,5=84,5
AC=2,4*CB=2,4*32,5=78
R=(AC+CB-AB)/2, тогда получаем:
R=(78+32,5-84,5)/2=13.
Ответ: R=13.
Поделитесь решением
Присоединяйтесь к нам...
 Точка H является основанием высоты
BH, проведенной из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите PK, если BH=16.
Точка H является основанием высоты
BH, проведенной из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите PK, если BH=16.
 В треугольнике ABC известно, что AB=BC, ∠ABC=102°. Найдите угол BCA. Ответ дайте в градусах.
В треугольнике ABC известно, что AB=BC, ∠ABC=102°. Найдите угол BCA. Ответ дайте в градусах.
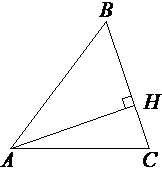 В остроугольном треугольнике ABC высота AH равна 20√
В остроугольном треугольнике ABC высота AH равна 20√
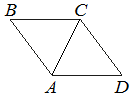 В ромбе ABCD угол ABC равен 72°. Найдите угол ACD. Ответ дайте в градусах.
В ромбе ABCD угол ABC равен 72°. Найдите угол ACD. Ответ дайте в градусах.
 Прямая AD, перпендикулярная медиане ВМ треугольника АВС, делит угол ВАС пополам. Найдите сторону АС, если сторона АВ равна 3.
Прямая AD, перпендикулярная медиане ВМ треугольника АВС, делит угол ВАС пополам. Найдите сторону АС, если сторона АВ равна 3.
Комментарии: