Укажите номера верных утверждений.
1) Существует ромб, который не является квадратом.
2) Если две стороны треугольника равны, то равны и противолежащие им углы.
3) Касательная к окружности параллельна радиусу, проведённому в точку касания.
Рассмотрим каждое утверждение:
1) "Существует ромб, который не является квадратом".
Ромб будет
квадратом только в одном случае - если все углы ромба будут равны 90°. При других значениях углов ромб не будет квадратом. Следовательно, это утверждение верно.
2) "Если две стороны треугольника равны, то равны и противолежащие им углы", это утверждение верно, т.к. это утверждение соответствует
свойству
равнобедренного треугольника.
3) "Касательная к окружности параллельна радиусу, проведённому в точку касания", это утверждение неверно, т.к. противоречит
свойству
касательной.
Поделитесь решением
Присоединяйтесь к нам...
В параллелограмме ABCD диагонали AC и BD пересекаются в точке M. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника AMD.
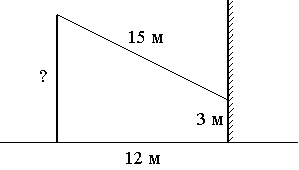От столба к дому натянут провод длиной 17 м, который закреплён на стене дома на высоте 4 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 15 м.
Найдите площадь параллелограмма, изображённого на рисунке.
Вершины ромба расположены на сторонах параллелограмма, а стороны ромба параллельны диагоналям параллелограмма. Найдите отношение площадей ромба и параллелограмма, если отношение диагоналей параллелограмма равно 28.
Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=11 и MB=16. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: