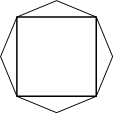
Дан правильный восьмиугольник. Докажите, что если его вершины последовательно соединить отрезками через одну, то получится квадрат.
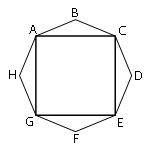Рассмотрим треугольники ABC, CDE, EFG и GHA. AB=BC=CD=DE=EF=FG=GH=HA (по
определению правильного многоугольника).
/ABC=/CDE=/EFG=/GHA (по
определению правильного многоугольника).
Следовательно, рассматриваемые треугольники равны (по
первому признаку равенства треугольников).
Это означает, что AC=CE=EG=GA.
Из равенства этих треугольников также следует, что все их острые углы тоже равны (/BAC=/BCA=/DCE=...и т.д.). Следовательно, /ACE=/CEG=/EGA=/GAC.
В итоге, по
определению правильного многоугольника получается, что ACEG - правильный многоугольник. А т.к. этот многоугольник имеет 4 угла, то это
квадрат.
Поделитесь решением
Присоединяйтесь к нам...
В равнобедренной трапеции известны высота, меньшее основание и угол при основании. Найдите большее основание.
Сторона ромба равна 40, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB=BC и ∠ABC=79°. Найдите величину угла BOC. Ответ дайте в градусах.
В треугольнике ABC угол A равен 45°, угол B равен 30°, BC=6√
На какой угол (в градусах) поворачивается минутная стрелка, пока часовая проходит 21°?
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: