
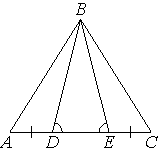
 На стороне АС треугольника АВС выбраны точки D и E так, что отрезки AD и CE равны (см. рисунок). Оказалось, что углы АEB и BDC тоже равны. Докажите, что треугольник АВС — равнобедренный.
На стороне АС треугольника АВС выбраны точки D и E так, что отрезки AD и CE равны (см. рисунок). Оказалось, что углы АEB и BDC тоже равны. Докажите, что треугольник АВС — равнобедренный.
1) По условию задачи /BED=/EDB, следовательно треугольник BDE - равнобедренный (по
свойству). По
определению равнобедренного треугольника BE=BD.
Смежные углы для углов /BED и /EDB тоже равны, /BDA=/BEC.
2) Рассмотрим треугольники ABD и CBE.
AD=EC (по условию),
BE=BD (согласно п.1),
/BDA=/BEC (из п.1),
следовательно эти треугольники равны (по
первому признаку равенства треугольников), а это значит, что BA=BC. Следовательно треугольник ABC - равнобедренный (по
определению).
Поделитесь решением
Присоединяйтесь к нам...
 Длина хорды окружности равна 130, а расстояние от центра окружности до этой хорды равно 72. Найдите диаметр окружности.
Длина хорды окружности равна 130, а расстояние от центра окружности до этой хорды равно 72. Найдите диаметр окружности.
Синус острого угла A треугольника ABC равен 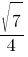 . Найдите CosA.
. Найдите CosA.
 Диагонали AC и BD трапеции ABCD с основаниями BC и AD пересекаются в точке O, BC=3, AD=7, AC=20. Найдите AO.
Диагонали AC и BD трапеции ABCD с основаниями BC и AD пересекаются в точке O, BC=3, AD=7, AC=20. Найдите AO.
Через середину K медианы BM треугольника ABC и вершину A проведена прямая, пересекающая сторону BC в точке P. Найдите отношение площади треугольника ABC к площади четырёхугольника KPCM.
 На стороне BC прямоугольника ABCD, у которого AB=12 и AD=17, отмечена точка E так, что
/EAB=45°. Найдите ED.
На стороне BC прямоугольника ABCD, у которого AB=12 и AD=17, отмечена точка E так, что
/EAB=45°. Найдите ED.
Комментарии: