
Укажите номера верных утверждений.
1) Центр вписанной окружности равнобедренного треугольника лежит на высоте, проведённой к основанию треугольника.
2) Ромб не является параллелограммом.
3) Сумма острых углов прямоугольного треугольника равна 90°.
Рассмотрим каждое утверждение:
1) "Центр вписанной окружности равнобедренного треугольника лежит на высоте, проведённой к основанию треугольника". Центр
вписанной окружности любого треугольника - точка пересечения
биссектрис (по
свойству вписанной окружности). А в
равнобедренном треугольнике высота, проведенная к основанию является и
биссектрисой и медианой (
свойство). Следовательно, это утверждение верно.
2) "Ромб не является параллелограммом", это утверждение неверно, т.к. противоречит
определению ромба.
3) "Сумма острых углов прямоугольного треугольника равна 90°". В теореме о сумме углов треугольника говорится, что сумма всех углов треугольника равна 180°. В прямоугольном треугольнике один из углов равен 90°, следовательно, сумма двух оставшихся углов равна 180°-90°=90°. Т.е. это утверждение верно.
Поделитесь решением
Присоединяйтесь к нам...
 Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках K и M соответственно. Найдите AC, если BK:KA=1:2, KM=23.
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках K и M соответственно. Найдите AC, если BK:KA=1:2, KM=23.
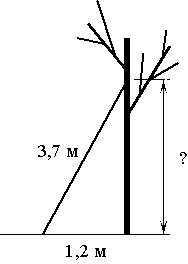 Лестницу длиной 3,7 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 1,2 м?
Лестницу длиной 3,7 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 1,2 м?
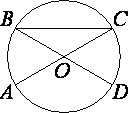 В окружности с центром O отрезки AC и BD — диаметры. Центральный угол AOD равен 130°. Найдите вписанный угол ACB. Ответ дайте в градусах.
В окружности с центром O отрезки AC и BD — диаметры. Центральный угол AOD равен 130°. Найдите вписанный угол ACB. Ответ дайте в градусах.
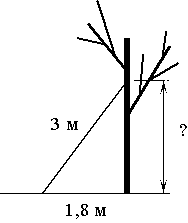 Лестницу длиной 3 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 1,8 м?
Лестницу длиной 3 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 1,8 м?
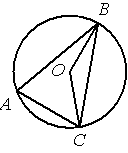 Точка О – центр окружности, /BAC=70° (см. рисунок). Найдите величину угла BOC (в градусах).
Точка О – центр окружности, /BAC=70° (см. рисунок). Найдите величину угла BOC (в градусах).
Комментарии: