Центральный угол AOB равен
60°. Найдите длину хорды AB, на которую он опирается, если радиус окружности равен 7.
Рассмотрим треугольник АОВ. АО=ОВ, т.к. это радиусы окружности. Следовательно,
треугольник АОВ - равнобедренный. Следовательно, /ОВА = /ОАВ (по свойству равнобедренного треугольника).
По теореме о сумме углов треугольника можем записать:
180°=/AOB+/OBA+/BAO
180°=60°+/OBA+/BAO
120°=/OBA+/BAO
А так как /OBA=/BAO, то /OBA=/BAO=120°/2=60°.
Следовательно треугольник АОВ - равносторонний (по свойству равностороннего треугольника). Следовательно, ОВ=ОА=АВ=7.
Ответ: АВ=7.
Поделитесь решением
Присоединяйтесь к нам...
Укажите номера верных утверждений.
1) Центр вписанной окружности равнобедренного треугольника лежит на высоте, проведённой к основанию треугольника.
2) Ромб не является параллелограммом.
3) Сумма острых углов прямоугольного треугольника равна 90°.
Найдите площадь треугольника, изображённого на рисунке.
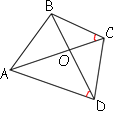В выпуклом четырёхугольнике ABCD углы BCA и BDA равны. Докажите, что углы ABD и ACD также равны.
Медиана BM и биссектриса AP треугольника ABC пересекаются в точке K, длина стороны AC втрое больше длины стороны AB. Найдите отношение площади треугольника AKM к площади четырёхугольника KPCM.
Сторона квадрата равна 9√2. Найдите диагональ этого квадрата.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: