
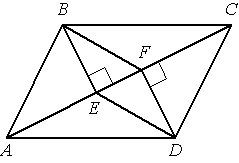
 В параллелограмме АВСD проведены перпендикуляры ВЕ и DF к диагонали АС (см. рисунок). Докажите, что треугольники BEF и DFE равны.
В параллелограмме АВСD проведены перпендикуляры ВЕ и DF к диагонали АС (см. рисунок). Докажите, что треугольники BEF и DFE равны.
1) Рассмотрим треугольники ABE и CDF.
AB=CD (по
свойству параллелограмма).
/BAE=/DCF (т.к. это
внутренние накрест-лежащие углы для параллельных BC и AD и секущей AC).
/BEA=/DFC (т.к. оба эти угла прямые по условию).
Если два угла у данных треугольников попарно равны, то и третьи углы равны (по
теореме о сумме углов треугольника).
Следовательно треугольники ABE и CDF равны (по
второму признаку равенства треугольников). Отсюда следует, что BE=FD
2) Рассмотрим треугольники BFE и DEF.
BE=FD (из пункта 1), EF-общая сторона, /BEF=/DFE (т.к. это прямые углы по условию).
Следовательно треугольники BFE и DEF равны (по
первому признаку равенства треугольников).
Поделитесь решением
Присоединяйтесь к нам...
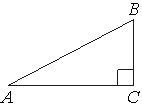 В треугольнике ABC угол C равен 90°, BC=3, AB=5. Найдите cosB.
В треугольнике ABC угол C равен 90°, BC=3, AB=5. Найдите cosB.
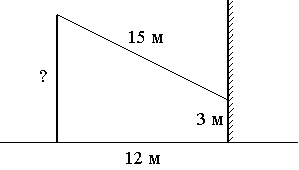 От столба к дому натянут провод длиной 15 м, который закреплён на стене дома на высоте 3 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 12 м.
От столба к дому натянут провод длиной 15 м, который закреплён на стене дома на высоте 3 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 12 м.
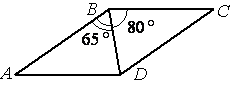 Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 65° и 80°. Найдите меньший угол параллелограмма.
Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 65° и 80°. Найдите меньший угол параллелограмма.
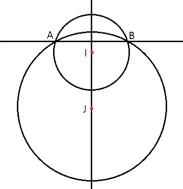 Окружности с центрами в точках I и J пересекаются в точках A и B, причём точки I и J лежат по одну сторону от прямой AB. Докажите, что AB⊥IJ.
Окружности с центрами в точках I и J пересекаются в точках A и B, причём точки I и J лежат по одну сторону от прямой AB. Докажите, что AB⊥IJ.
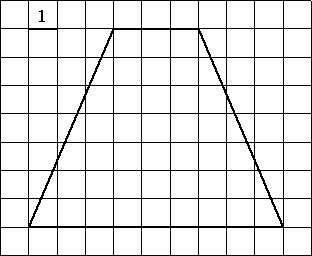 Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке.
Комментарии: