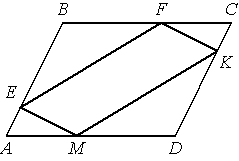
В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём АЕ = CK, СF = АM. Докажите, что EFKM — параллелограмм.
1) Рассмотрим треугольники АЕМ и CKF.
АЕ=CK (по условию задачи)
/A=/C (по
свойству параллелограмма)
СF=АM (по условию задачи).
Следовательно, треугольники АЕМ и CKF равны (по первому признаку).
Поэтому ЕМ=FK.
2) Рассмотрим треугольники EBF и KDM.
Т.к. AB=CD и AD=BC (по
свойству параллелограмма), а АЕ = CK и СF = АM (по условию задачи), то BE=KD и BF=DM.
/B=/D (по
свойству параллелограмма).
Следовательно, треугольники EBF и KDM (по первому признаку). А это значит, что EF=KM.
Из пунктов 1 и 2 (равенство сторон) следует, что EFKM —
параллелограмм (по
свойству параллелограмма).
Поделитесь решением
Присоединяйтесь к нам...
Косинус острого угла A треугольника ABC равен 
. Найдите sinA.
Точка О – центр окружности, /AOB=130° (см. рисунок). Найдите величину угла
ACB (в градусах).
Точка O – центр окружности, на которой лежат точки A, B и C. Известно, что ∠ABC=43° и ∠OAB=13°. Найдите угол BCO. Ответ дайте в градусах.
Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF=8, BF=15.
Центральный угол AOB опирается на хорду АВ длиной 5. При этом угол ОАВ равен 60°. Найдите радиус окружности.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: