Найдите угол ABC равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной CD углы, равные 30° и 80° соответственно.
Угол ∠BCA=∠CAD, т.к. это
внутренние накрест-лежащие углы.
Следовательно, ∠BCD=80°+30°=110°.
По
свойству равнобедренной трапеции ∠BCD=∠ABC=110°.
Ответ: ∠ABC=110°
Поделитесь решением
Присоединяйтесь к нам...
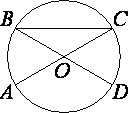В окружности с центром O отрезки AC и BD — диаметры. Центральный угол AOD равен 132°. Найдите вписанный угол ACB. Ответ дайте в градусах.
Радиус окружности, описанной около равностороннего треугольника, равен 10√3. Найдите длину стороны этого треугольника.
Стороны AC, AB, BC треугольника ABC равны 2√
В трапеции ABCD основания AD и BC равны соответственно 49 и 21, а сумма углов при основании AD равна 90°. Найдите радиус окружности, проходящей через точки A и B и касающейся прямой CD, если AB=20.
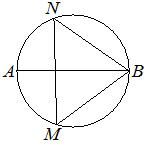На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠NBA=36°. Найдите угол NMB. Ответ дайте в градусах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2021-10-04 12:42:21) Администратор: Потому, что AB не параллельна CD.
(2021-09-30 09:52:25) : а почему угла BAC и ACD не являются накрест лежащими?