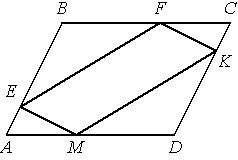
В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём СF = АM, BE = DK. Докажите, что EFKM — параллелограмм.
Рассмотрим треугольники АЕМ и CKF.
АM = CF (по условию задачи)
/A=/C (по
свойству параллелограмма)
Т.к. AB=CD (по
свойству параллелограмма), а BE = DK (по условию), то АE=CK.
Следовательно, треугольники АЕМ и CKF равны (по первому признаку).
Поэтому ЕМ=FK.
Аналогично доказывается, что треугольники EBF и KDM тоже равны, следовательно EF=MK.
Т.е. противоположные стороны данного четырехугольника равны. Соответственно этот четырехугольник - параллелограмм (по
свойству параллелограмма).
Поделитесь решением
Присоединяйтесь к нам...
Боковая сторона трапеции равна 5, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 3 и 9.
Точка O – центр окружности, на которой лежат точки A, B и C. Известно, что ∠ABC=15° и ∠OAB=8°. Найдите угол BCO. Ответ дайте в градусах.
Какие из данных утверждений верны? Запишите их номера.
1) Против большей стороны треугольника лежит больший угол.
2) Любой прямоугольник можно вписать в окружность.
3) Площадь треугольника меньше произведения двух его сторон.
В треугольнике ABC AB=BC, а высота AH делит сторону BC на отрезки BH=48 и CH=2. Найдите cosB.
В треугольнике ABC биссектриса угла A делит высоту, проведенную из вершины B в отношении 5:3, считая от точки B. Найдите радиус окружности, описанной около треугольника ABC, если BC=8.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: