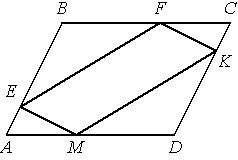
В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём СF = АM, BE = DK. Докажите, что EFKM — параллелограмм.
Рассмотрим треугольники АЕМ и CKF.
АM = CF (по условию задачи)
/A=/C (по
свойству параллелограмма)
Т.к. AB=CD (по
свойству параллелограмма), а BE = DK (по условию), то АE=CK.
Следовательно, треугольники АЕМ и CKF равны (по первому признаку).
Поэтому ЕМ=FK.
Аналогично доказывается, что треугольники EBF и KDM тоже равны, следовательно EF=MK.
Т.е. противоположные стороны данного четырехугольника равны. Соответственно этот четырехугольник - параллелограмм (по
свойству параллелограмма).
Поделитесь решением
Присоединяйтесь к нам...
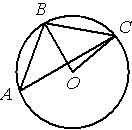Точка О – центр окружности, /BAC=40° (см. рисунок). Найдите величину угла BOC (в градусах).
В треугольнике ABC известно, что AB=8, BC=10, AC=12. Найдите cos∠ABC.
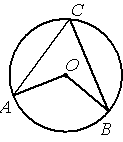Точка О – центр окружности, /AOB=128° (см. рисунок). Найдите величину угла ACB (в градусах).
В треугольнике со сторонами 2 и 4 проведены высоты к этим сторонам. Высота, проведённая к первой стороне, равна 2. Чему равна высота, проведённая ко второй стороне?
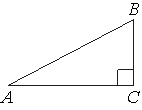В треугольнике ABC угол C равен 90°, tgB=7/6, BC=18. Найдите AC.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: