Укажите номера верных утверждений.
1) Существует прямоугольник, который не является параллелограммом.
2) Треугольник с углами 40° , 70°, 70° — равнобедренный.
3) Если из точки M проведены две касательные к окружности и А и В — точки касания, то отрезки MA и MB равны.
Рассмотрим каждое утверждение:
1) "Существует прямоугольник, который не является параллелограммом", это утверждение неверно, т.к. любой
прямоугольник полностью удовлетворяет
определению параллелограмма.
2) "Треугольник с углами 40° , 70°, 70° — равнобедренный", это утверждение верно, по
свойству
равнобедренного треугольника.
3) "Если из точки M проведены две касательные к окружности и А и В — точки касания, то отрезки MA и MB равны". MA и MB -
касательные, тогда, по второму свойству касательной, это утверждение верно.
Поделитесь решением
Присоединяйтесь к нам...
В параллелограмме ABCD диагональ AC в 2 раза больше стороны AB и ∠ACD=1°. Найдите угол между диагоналями параллелограмма. Ответ дайте в градусах.
В треугольнике два угла равны 43° и 88°. Найдите его третий угол. Ответ дайте в градусах.
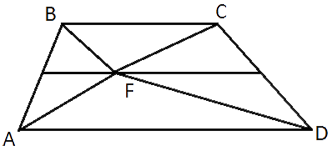На средней линии трапеции ABCD с основаниями AD и BC выбрали произвольную точку F. Докажите, что сумма площадей треугольников BFC и AFD равна половине площади трапеции.
Радиус окружности, вписанной в трапецию, равен 48. Найдите высоту этой трапеции.
Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=7 и MB=17. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: