
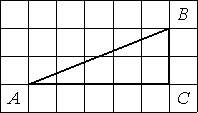
 Найдите тангенс угла В треугольника ABC, изображённого на рисунке.
Найдите тангенс угла В треугольника ABC, изображённого на рисунке.
По
определению тангенса: tgB=AC/CB=5/2=2,5.
Ответ: tgB=2,5.
Поделитесь решением
Присоединяйтесь к нам...
 Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно. Найдите BN, если MN=15, AC=25, NC=22.
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно. Найдите BN, если MN=15, AC=25, NC=22.
 Найдите больший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной АВ углы, равные 30° и 45° соответственно. Ответ дайте в градусах.
Найдите больший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной АВ углы, равные 30° и 45° соответственно. Ответ дайте в градусах.
Основание AC равнобедренного треугольника ABC равно 10. Окружность радиуса 8 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
 В треугольнике ABC известно, что AB=8, BC=10, AC=12. Найдите cos∠ABC.
В треугольнике ABC известно, что AB=8, BC=10, AC=12. Найдите cos∠ABC.
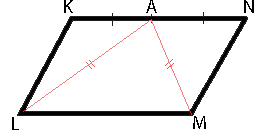 В параллелограмме KLMN точка A — середина стороны KN. Известно, что AL=AM. Докажите, что данный параллелограмм — прямоугольник.
В параллелограмме KLMN точка A — середина стороны KN. Известно, что AL=AM. Докажите, что данный параллелограмм — прямоугольник.
Комментарии: