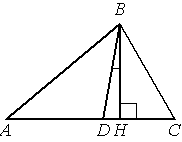
В треугольнике АВС углы А и С равны 40° и 60° соответственно. Найдите угол между высотой ВН и биссектрисой BD.
По
теореме о сумме углов треугольника: 180°=/A+/B+/C, отсюда /B=180°-/A-/C=180°-40°-60°=80°.
/ABD=/B/2=40° (т.к. BD -
биссектриса).
Рассмотрим треугольник BHC, по
теореме о сумме углов треугольника получаем 180°=60°+90°+/CBH => /CBH=30°.
Тогда искомый угол /DBH=/B-/ABD-/CBH=80°-40°-30°=10°.
Ответ: /DBH=10°
Поделитесь решением
Присоединяйтесь к нам...
Укажите номера верных утверждений.
1) Существует ромб, который не является квадратом.
2) Если две стороны треугольника равны, то равны и противолежащие им углы.
3) Касательная к окружности параллельна радиусу, проведённому в точку касания.
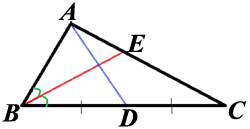В треугольнике ABC биссектриса BE и медиана AD перпендикулярны
и имеют одинаковую длину, равную 44. Найдите стороны треугольника ABC.
Диагонали AC и BD трапеции ABCD с основаниями BC и AD пересекаются в точке O, BC=3, AD=5, AC=24. Найдите AO.
В параллелограмме ABCD диагонали AC и BD пересекаются в точке M. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника CMD.
В треугольнике ABC угол C равен 90°, tgB=3/4, BC=12. Найдите AC.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: