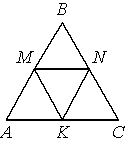
В равностороннем треугольнике ABC точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что АMNK — ромб.
По условию задачи AB=BC=CA (т.к. треугольник ABC -
равносторонний). Значит AK=KC=CN=NB=BM=MA.
Тогда, MN -
средняя линия треугольника ABC. Следовательно, MN=AK и MN||AK (по
теореме о средней линии).
NK - тоже
средняя линия, равна AM и параллельна AM.
Получается, что AM=MN=NK=KA, т.е. AMNK -
ромб (по
свойству ромба).
Поделитесь решением
Присоединяйтесь к нам...
Четырёхугольник ABCD описан около окружности, AB=9, BC=13, CD=18. Найдите AD.
В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 25, 8 и 7. Найдите площадь параллелограмма ABCD.
Найдите площадь треугольника, изображённого на рисунке.
В остроугольном треугольнике ABC проведена высота BH, ∠BAC=37°. Найдите угол ABH. Ответ дайте в градусах.
Одна из биссектрис треугольника делится точкой пересечения биссектрис в отношении 26:1, считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна 7.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: