Укажите номера верных утверждений.
1) Медиана равнобедренного треугольника, проведённая из вершины угла, противолежащего основанию, делит этот угол пополам.
2) Не существует прямоугольника, диагонали которого взаимно перпендикулярны.
3) В плоскости для точки, лежащей вне круга, расстояние до центра круга больше его радиуса.
Рассмотрим каждое утверждение:
1) "Медиана
равнобедренного треугольника, проведённая из вершины угла, противолежащего основанию, делит этот угол пополам", это утверждение верно (по
свойству равнобедренного треугольника).
2) "Не существует прямоугольника, диагонали которого взаимно перпендикулярны", это утверждение неверно,
квадрат - такой
прямоугольник.
3) "В плоскости для точки, лежащей вне круга, расстояние до центра круга больше его радиуса", это утверждение верно. Это очевидно, если провести отрезок через центр
окружности и данную точку, радиус будет меньше этого отрезка.
Поделитесь решением
Присоединяйтесь к нам...
В трапецию, сумма длин боковых сторон которой равна 30, вписана окружность. Найдите длину средней линии трапеции.
На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠NBA=69°. Найдите угол NMB. Ответ дайте в градусах.
В окружности с центром O AC и BD – диаметры. Центральный угол AOD равен 128°. Найдите вписанный угол ACB. Ответ дайте в градусах.
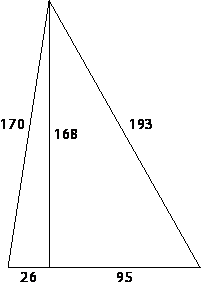Найдите площадь треугольника, изображённого на рисунке.
Косинус острого угла A треугольника ABC равен 
. Найдите sinA.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2017-01-10 22:30:29) Администратор: Нет, конечно. Смежные углы характерны тем, что их сумма равна 180 градусов. А вот вертикальные углы равны.
(2017-01-10 19:47:24) : смежные углы равны?