
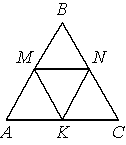
 В равностороннем треугольнике ABC точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что ВMKN — ромб.
В равностороннем треугольнике ABC точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что ВMKN — ромб.
По условию задачи AB=BC=CA (т.к. треугольник ABC -
равносторонний). Значит AK=KC=CN=NB=BM=MA.
Тогда, MK -
средняя линия треугольника ABC. Следовательно, MK=BN и MK||BN (по
теореме о средней линии).
NK - тоже
средняя линия, равна BM и параллельна BM.
Получается, что MK=BN=BM=NK, т.е. BMNK -
ромб (по
свойству ромба).
Поделитесь решением
Присоединяйтесь к нам...
Какие из данных утверждений верны? Запишите их номера.
1) Против большей стороны треугольника лежит меньший угол.
2) Любой квадрат можно вписать в окружность.
3) Площадь трапеции равна произведению средней линии на высоту.
 В треугольнике ABC AB=BC=53, AC=56. Найдите длину медианы BM.
В треугольнике ABC AB=BC=53, AC=56. Найдите длину медианы BM.
 В треугольнике ABC известны длины сторон AB=30, AC=100, точка O — центр окружности, описанной около треугольника ABC. Прямая BD, перпендикулярная прямой AO, пересекает сторону AC в точке D.
Найдите CD.
В треугольнике ABC известны длины сторон AB=30, AC=100, точка O — центр окружности, описанной около треугольника ABC. Прямая BD, перпендикулярная прямой AO, пересекает сторону AC в точке D.
Найдите CD.
 Длина хорды окружности равна 60, а расстояние от центра окружности до этой хорды равно 40. Найдите диаметр окружности.
Длина хорды окружности равна 60, а расстояние от центра окружности до этой хорды равно 40. Найдите диаметр окружности.
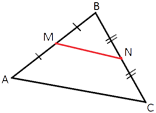 Точки M и N являются серединами сторон AB и BC треугольника ABC, AC=42. Найдите MN.
Точки M и N являются серединами сторон AB и BC треугольника ABC, AC=42. Найдите MN.
Комментарии: