
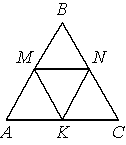
 В равностороннем треугольнике ABC точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что ВMKN — ромб.
В равностороннем треугольнике ABC точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что ВMKN — ромб.
По условию задачи AB=BC=CA (т.к. треугольник ABC -
равносторонний). Значит AK=KC=CN=NB=BM=MA.
Тогда, MK -
средняя линия треугольника ABC. Следовательно, MK=BN и MK||BN (по
теореме о средней линии).
NK - тоже
средняя линия, равна BM и параллельна BM.
Получается, что MK=BN=BM=NK, т.е. BMNK -
ромб (по
свойству ромба).
Поделитесь решением
Присоединяйтесь к нам...
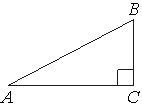 В треугольнике ABC угол C равен 90°, BC=3, AB=5. Найдите cosB.
В треугольнике ABC угол C равен 90°, BC=3, AB=5. Найдите cosB.
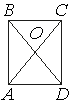 Диагонали AC и BD прямоугольника ABCD пересекаются
в точке O, BO=37, AB=56. Найдите AC.
Диагонали AC и BD прямоугольника ABCD пересекаются
в точке O, BO=37, AB=56. Найдите AC.
 Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=17 и MB=19. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=17 и MB=19. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
 Найдите острые углы прямоугольного треугольника, если его гипотенуза равна 16, а площадь равна 32√
Найдите острые углы прямоугольного треугольника, если его гипотенуза равна 16, а площадь равна 32√
 Площадь прямоугольного треугольника равна 50√
Площадь прямоугольного треугольника равна 50√
Комментарии: