Укажите номера верных утверждений.
1) Биссектриса равнобедренного треугольника, проведённая из вершины, противолежащей основанию, перпендикулярна основанию.
2) Диагонали ромба точкой пересечения делятся пополам.
3) Из двух хорд окружности больше та, середина которой находится дальше от центра окружности.
Рассмотрим каждое утверждение.
1) "
Биссектриса
равнобедренного треугольника, проведённая из вершины, противолежащей основанию, перпендикулярна основанию", это утверждение верно, по
свойству равнобедренного треугольника - такая
биссектриса является и медианой, и высотой, следовательно, она перпендикулярна основанию.
2) "Диагонали
ромба точкой пересечения делятся пополам", это утверждение верно, т.к. это утверждение является
свойством параллелограмма, а
ромб - это тоже
параллелограмм.
3) "Из двух хорд окружности больше та, середина которой находится дальше от центра окружности", это утверждение неверно. Диаметр - это наибольшая
хорда, следовательно, чем центр хорды ближе к центру окружности, тем хорда больше.
Поделитесь решением
Присоединяйтесь к нам...
Синус острого угла A треугольника ABC равен √
Вершины ромба расположены на сторонах параллелограмма, а стороны ромба параллельны диагоналям параллелограмма. Найдите отношение площадей ромба и параллелограмма, если отношение диагоналей параллелограмма равно 31.
Найдите площадь треугольника, изображённого на рисунке.
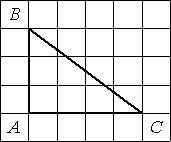Найдите тангенс угла С треугольника ABC, изображённого на рисунке.
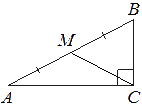В треугольнике ABC угол C равен 90°, M — середина стороны AB, AB=20, BC=10. Найдите CM.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: