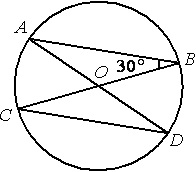В окружности с центром в точке О проведены диаметры AD и BC, угол
ABO равен 30°. Найдите величину угла ODC.
Вариант 1. Предложил пользователь Татьяна.
∠ABO=∠ABC=30°
∠ODC=∠ADC
Оба этих угла являются
вписанными и опираются на одну и ту же дугу, следовательно (по
второму свойству) они равны:
∠ABC=∠ADC=∠ODC=30°
Ответ: 30
Вариант 2.
Рассмотрим треугольник ABO. Этот треугольник
равнобедренный, т.к. ОA и ОB - радиусы, поэтому они равны.
По
свойству равнобедренного треугольника /OAB=/OBA.
Рассмотрим треугольники АОВ и COD. /DOC=/AOB, т.к. они
вертикальные. СО=DO=OB=OA, т.к. это радиусы окружности.
Следовательно, треугольники АОВ и COD равны (по
первому признаку). Поэтому /OBA=/OAB=/ODC=/OCD=30°
Ответ: /ODC=30°.
Поделитесь решением
Присоединяйтесь к нам...
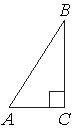В треугольнике ABC угол C равен 90°, sinB=3/5, AB=10. Найдите AC.
Катеты прямоугольного треугольника равны
√
Диагональ прямоугольника образует угол 75° с одной из его сторон. Найдите угол между диагоналями этого прямоугольника. Ответ дайте в градусах.
Укажите номера верных утверждений.
1) Центр описанной окружности равнобедренного треугольника лежит на высоте, проведённой к основанию треугольника.
2) Квадрат является прямоугольником.
3) Сумма углов любого треугольника равна
180°.
Центральный угол AOB опирается на хорду АВ длиной 5. При этом угол ОАВ равен 60°. Найдите радиус окружности.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2014-11-29 23:20:48) Администратор: Татьяна, да, Вы совершенно правы. Я добавлю Ваш вариант решения на сайт.
(2014-11-29 23:09:15) Татьяна: А нельзя ли эту задачу решить проще?Ведь угол ОДС и АВО - вписанные и опирающиеся на одну дугу. Следовательно, они равны, поэтому угол ОДС=30 градусов.