
 В равнобедренном треугольнике ABC (АВ=ВС) точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что треугольник MNK — равнобедренный.
В равнобедренном треугольнике ABC (АВ=ВС) точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что треугольник MNK — равнобедренный.
NK - является
средней линией треугольника ABC и равна половине AB.
MK - является
средней линией треугольника ABC и равна половине BC.
Т.к. AB=BC (по условию), то NK=MK.
Следовательно треугольник MNK -
равнобедренный.
Поделитесь решением
Присоединяйтесь к нам...
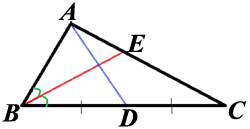 В треугольнике ABC биссектриса BE и медиана AD перпендикулярны
и имеют одинаковую длину, равную 44. Найдите стороны треугольника ABC.
В треугольнике ABC биссектриса BE и медиана AD перпендикулярны
и имеют одинаковую длину, равную 44. Найдите стороны треугольника ABC.
 Стороны AC, AB, BC треугольника ABC равны 2√
Стороны AC, AB, BC треугольника ABC равны 2√
 В треугольнике ABC проведена биссектриса AL, угол ALC равен 112°, угол ABC равен 106°. Найдите угол ACB. Ответ дайте в градусах.
В треугольнике ABC проведена биссектриса AL, угол ALC равен 112°, угол ABC равен 106°. Найдите угол ACB. Ответ дайте в градусах.
 Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 60° и 135°, а CD=36.
Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 60° и 135°, а CD=36.
 Найдите угол, который образуют минутная и часовая стрелки часов в 11:00. Ответ дайте в градусах.
Найдите угол, который образуют минутная и часовая стрелки часов в 11:00. Ответ дайте в градусах.
Комментарии: