Найдите меньший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной CD углы, равные
30° и 105° соответственно.
По свойству
равнобедренной трапеции - углы при основании равны. Тогда ∠CBA=30°+105°=135°.
Сумма углов четырехугольника равна 360°, тогда получаем, что 360°=135°+135°+∠BAD+∠ADC,
∠BAD+∠ADC=360°-135°-135°=90°, а учитывая, что ∠BAD=∠ADC (по тому
свойству равнобедренной трапеции), получаем ∠BAD=∠ADC=90°/2=45°, эти углы и есть меньшие в трапеции
Ответ: меньший угол трапеции = 45°.
Поделитесь решением
Присоединяйтесь к нам...
Укажите номера верных утверждений.
1) Если угол острый, то смежный с ним угол также является острым.
2) Диагонали квадрата взаимно перпендикулярны.
3) В плоскости все точки, равноудалённые от заданной точки, лежат на одной окружности.
Площадь прямоугольного треугольника равна 882√
Сторона равностороннего треугольника равна 10√
Радиус вписанной в квадрат окружности равен 24√2. Найдите радиус окружности, описанной около этого квадрата.
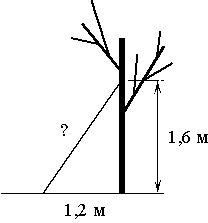Какова длина (в метрах) лестницы, которую прислонили к дереву, если верхний её конец находится на высоте 1,6 м над землёй, а нижний отстоит от ствола дерева на 1,2 м?
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2015-05-11 16:38:55) Администратор: Спасибо за найденную опечатку, исправлено!
(2015-05-11 14:37:16) : Есть ошибка. Не угол BAC, а угол BAD.
(2015-05-11 14:28:20) : Есть ошибка. Не угол BAC, а угол BAD.