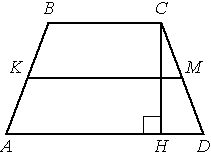
В трапеции АВСD боковые стороны AB и CD равны, СН — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 16, а меньшее основание BC равно 6.
Средняя линия трапеции Lср=(AD+BC)/2
Отсюда AD=2*Lср-BC.
Проведем еще одну высоту из вершины B
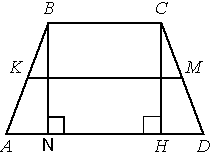и рассмотрим треугольники CDH и ABN.
AB=CD (по условию задачи)
BN=CH, т.к. BCHN -
прямоугольник, образованный параллельными сторонами трапеции и перпендикулярами к ним.
Следовательно, применив
теорему Пифагора, получим, что HD=NA
AD=AN+NH+HD
AD=2*HD+NH, NH=BC (т.к. BCHN - прямоугольник), тогда:
AD=2*HD+BC,
HD=(AD-BC)/2
Ранее мы выяснили, что AD=2*Lср-BC=2*16-6=26, тогда:
HD=(26-6)/2=10.
Ответ: 10
Поделитесь решением
Присоединяйтесь к нам...
Укажите номера верных утверждений.
1) Медиана равнобедренного треугольника, проведённая из вершины угла, противолежащего основанию, делит этот угол пополам.
2) Не существует прямоугольника, диагонали которого взаимно перпендикулярны.
3) В плоскости для точки, лежащей вне круга, расстояние до центра круга больше его радиуса.
Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 60° и 150°, а CD=33.
Точка O – центр окружности, на которой лежат точки S, T и V таким образом, что OSTV – ромб. Найдите угол OVT. Ответ дайте в градусах.
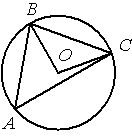Точка О – центр окружности, /BOC=100° (см. рисунок). Найдите величину угла BAC (в градусах).
В треугольнике ABC AB=BC=53, AC=56. Найдите длину медианы BM.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2018-01-19 20:09:01) Администратор: Вам что-то не нравится?
(2018-01-19 12:49:04) : это фуфло