В окружности с центром в точке О проведены диаметры AD и BC, угол OCD равен 75°. Найдите величину угла OAB.
Рассмотрим треугольник COD. Этот треугольник
равнобедренный, т.к. ОC и ОD - радиусы, поэтому они равны.
По
свойству равнобедренного треугольника /OCD=/ODC.
Рассмотрим треугольники АОВ и COD. /DOC=/AOB, т.к. они
вертикальные. СО=DO=OB=OA, т.к. это радиусы окружности.
Следовательно, треугольники АОВ и COD равны (по
первому признаку). Поэтому /OBA=/OAB=/ODC=/OCD=75°
Ответ: /OAB=75°.
Поделитесь решением
Присоединяйтесь к нам...
В треугольнике ABC известны длины сторон AB=30, AC=100, точка O — центр окружности, описанной около треугольника ABC. Прямая BD, перпендикулярная прямой AO, пересекает сторону AC в точке D.
Найдите CD.
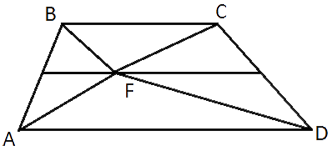На средней линии трапеции ABCD с основаниями AD и BC выбрали произвольную точку F. Докажите, что сумма площадей треугольников BFC и AFD равна половине площади трапеции.
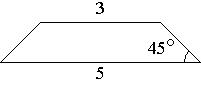В равнобедренной трапеции основания равны 3 и 5, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции.
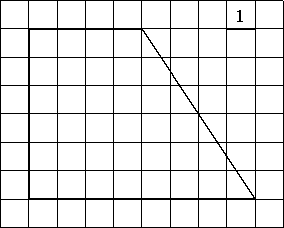Найдите площадь трапеции, изображённой на рисунке.
В треугольнике ABC AB=BC, а высота AH делит сторону BC на отрезки BH=3 и CH=1. Найдите cosB.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: