Укажите номера верных утверждений.
1) Биссектриса равнобедренного треугольника, проведённая из вершины, противолежащей основанию, делит основание на две равные части.
2) В любом прямоугольнике диагонали взаимно перпендикулярны.
3) Для точки, лежащей на окружности, расстояние до центра окружности равно радиусу.
Рассмотрим каждое утверждение.
1) "Биссектриса равнобедренного треугольника, проведённая из вершины, противолежащей основанию, делит основание на две равные части". По
свойству равнобедренного треугольника, такая
биссектриса является медианой. А медиана, по
определению, делит сторону пополам. Следовательно, это утверждение верно.
2) "В любом прямоугольнике диагонали взаимно перпендикулярны", это утверждение неверно. Нет такого
свойства.
3) "Для точки, лежащей на окружности, расстояние до центра окружности равно радиусу", это утверждение верно, по
определению.
Поделитесь решением
Присоединяйтесь к нам...
В параллелограмме ABCD диагонали AC и BD пересекаются в точке M. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника AMD.
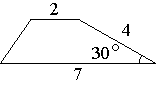Боковая сторона трапеции равна 4, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 2 и 7.
Укажите номера верных утверждений.
1) Центры вписанной и описанной окружностей равностороннего треугольника совпадают.
2) Существует квадрат, который не является ромбом.
3) Сумма углов остроугольного треугольника равна 180°.
Длина хорды окружности равна 60, а расстояние от центра окружности до этой хорды равно 40. Найдите диаметр окружности.
Диагональ прямоугольника образует угол 50° с одной из его сторон. Найдите угол между диагоналями этого прямоугольника. Ответ дайте в градусах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2017-04-30 22:07:28) Администратор: Мы не помогаем решить домашнее задание, цель сайта - подробно разобрать задачи, которые будут на экзаменах, чтобы учащиеся научились их решать самостоятельно. Если найдете похожую задачу на сайте fipi.ru, отправте заявку на добавление задачи, и мы ее обязательно добавим.
(2017-04-27 13:09:48) : Число кустов сирени в парке относится к числу кустов жасмина как 17 к 33 сколько процентов кустов парке составляет кусты сирени