ОГЭ, Математика.
Геометрия: Задача №4AEE60

Задача №172 из 1087
Условие задачи:

Сторона ромба равна 40, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?

Решение задачи:

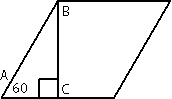Рассмотрим треугольник АВС, этот треугольник прямоугольный (по условию задачи). /A=60°, следовательно по теореме о сумме углов треугольника /АВС = 180°-90°-60°=30°. По свойству прямоугольного треугольника АС=АВ/2=40/2=20. Следовательно вторая половина стороны ромба = 40-20=20. Т.е., в данной задаче, высота, проведенная к стороне ромба делит эту сторону на две равные части.
Ответ: длины обоих отрезков равны 20.

Поделитесь решением

Присоединяйтесь к нам...

Вы можете поблагодарить автора, написать свои претензии или предложения на странице 'Про нас'

Другие задачи из этого раздела

Задача №276C90

Сторона ромба равна 32, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?

Задача №FFD85C

Укажите номера верных утверждений.
1) Существует ромб, который не является квадратом.
2) Если две стороны треугольника равны, то равны и противолежащие им углы.
3) Касательная к окружности параллельна радиусу, проведённому в точку касания.