
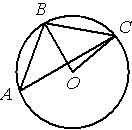
 Точка О – центр окружности, /BAC=40° (см. рисунок). Найдите величину угла BOC (в градусах).
Точка О – центр окружности, /BAC=40° (см. рисунок). Найдите величину угла BOC (в градусах).
По условию /BAC=40°, этот угол является
вписанным углом и равен половине дуги, на которую опирается (
по теореме о вписанном угле).
Следовательно, градусная мера дуги, в нашей задаче, равна 40°*2=80°.
/BOC является
центральным и равен градусной мере дуги, на которую опирается, следовательно, /BOC=80°.
Ответ: /BOC=80°.
Поделитесь решением
Присоединяйтесь к нам...
 В окружности с центром в точке О проведены диаметры AD и BC, угол
OCD равен 55°. Найдите величину угла OAB.
В окружности с центром в точке О проведены диаметры AD и BC, угол
OCD равен 55°. Найдите величину угла OAB.
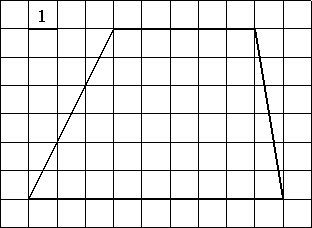 Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке.
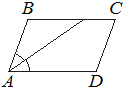 Найдите острый угол параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 41°. Ответ дайте в градусах.
Найдите острый угол параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 41°. Ответ дайте в градусах.
 Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 45° и 120°, а CD=40.
Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 45° и 120°, а CD=40.
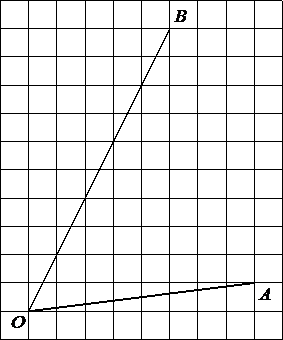 Найдите тангенс угла
AOB.
Найдите тангенс угла
AOB.
Комментарии: