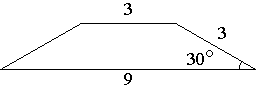
Боковая сторона трапеции равна 3, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 3 и 9.
Площадь
трапеции равна произведению полусуммы оснований на высоту. Основания нам известны, найдем высоту трапеции.
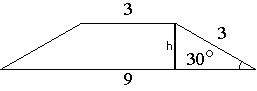
Проведем высоту как показано на рисунке. Получившийся треугольник является
прямоугольным. По
определению синуса можем записать: sin30°=h/3 => h=3*sin30°, sin30°=1/2 (
табличное значение).
h=3*1/2=1,5.
Sтрапеции=(3+9)/2*1,5=9
Ответ: площадь трапеции равна 9.
Поделитесь решением
Присоединяйтесь к нам...
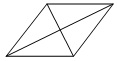Найдите площадь ромба, если его диагонали равны 39 и 2.
В окружности с центром в точке О проведены диаметры AD и BC, угол OCD равен 75°. Найдите величину угла OAB.
Из точки А проведены две касательные к окружности с центром в точке О. Найдите расстояние от точки А до точки О, если угол между касательными равен
60°, а радиус окружности равен 6.
В трапеции ABCD боковая сторона AB перпендикулярна основанию BC. Окружность проходит через точки C и D и касается прямой AB в точке E. Найдите расстояние от точки E до прямой CD, если AD=14, BC=7.
На каком расстоянии (в метрах) от фонаря стоит человек ростом 1,8 м, если длина его тени равна 9 м, высота фонаря 4 м?
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: