
 Сторона ромба равна 8, а расстояние от точки пересечения диагоналей ромба до неё равно 2. Найдите площадь этого ромба.
Сторона ромба равна 8, а расстояние от точки пересечения диагоналей ромба до неё равно 2. Найдите площадь этого ромба.
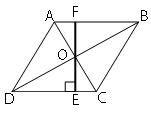 Обозначим ключевые точки как показано на рисунке.
Обозначим ключевые точки как показано на рисунке.
Проведем продолжение высоты OE к стороне AB и обозначим точку пересечения как F (как показано на рисунке).
Площадь
ромба (как и
параллелограмма) равна произведению высоты на сторону ромба.
Высота ромба = EF (т.к. EF перпендикулярна CD). Рассмотрим треугольники DOE и BOF.
DO=OB (по второму
свойству ромба)
∠DOE=∠BOE (т.к. они
вертикальные)
∠EDO=∠FBO (т.к. это
внутренние накрест-лежащие)
Следовательно, треугольники DOE и BOF равны по
второму признаку.
Тогда OE=OF => EF=2*OE=2*2=4
Sромба=EF*CD=4*8=32
Ответ: Sромба=32
Поделитесь решением
Присоединяйтесь к нам...
 Найдите площадь треугольника, изображённого на рисунке.
Найдите площадь треугольника, изображённого на рисунке.
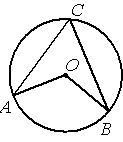 Точка О – центр окружности, /AOB=130° (см. рисунок). Найдите величину угла
ACB (в градусах).
Точка О – центр окружности, /AOB=130° (см. рисунок). Найдите величину угла
ACB (в градусах).
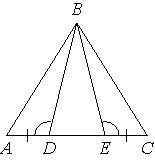 На стороне АС треугольника АВС выбраны точки D и E так, что отрезки AD и CE равны (см. рисунок). Оказалось, что углы АDB и BEC тоже равны. Докажите, что треугольник АВС — равнобедренный.
На стороне АС треугольника АВС выбраны точки D и E так, что отрезки AD и CE равны (см. рисунок). Оказалось, что углы АDB и BEC тоже равны. Докажите, что треугольник АВС — равнобедренный.
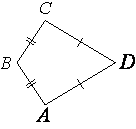 В выпуклом четырехугольнике ABCD известно, что AB=BC, AD=CD, ∠B=133°, ∠D=173°. Найдите
угол A. Ответ дайте в градусах.
В выпуклом четырехугольнике ABCD известно, что AB=BC, AD=CD, ∠B=133°, ∠D=173°. Найдите
угол A. Ответ дайте в градусах.
 Радиус вписанной в квадрат окружности равен 4√2. Найдите диагональ этого квадрата.
Радиус вписанной в квадрат окружности равен 4√2. Найдите диагональ этого квадрата.
Комментарии:
(2022-11-20 14:01:01) Артемий: докажите, что четырехугольник изображенный на клетчатой бумаге имеет два равных угла