Синус острого угла A треугольника ABC равен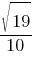 
. Найдите CosA.
Так как нам ничего не известно про треугольник ABC, прямоугольный он или нет и т.д. То остается только воспользоваться основной тригонометрической формулой:
sin2A+cos2A=1
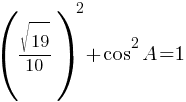
По второму правилу действий со степенями:
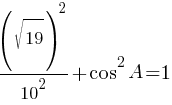
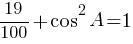
0,19+cos2A=1
cos2A=1-0,19
cos2A=0,81
cosA=√0,81=0,9
Ответ: 0,9
Поделитесь решением
Присоединяйтесь к нам...
Какие из данных утверждений верны? Запишите их номера.
1) Если при пересечении двух прямых третьей прямой накрест лежащие углы равны, то прямые параллельны.
2) Диагональ трапеции делит её на два равных треугольника.
3) Если в ромбе один из углов равен
90°, то такой ромб — квадрат.
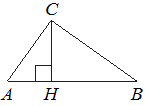На гипотенузу AB прямоугольного треугольника ABC опущена высота CH, AH=2, BH=18. Найдите CH.
Точка О – центр окружности, /ACB=25° (см. рисунок). Найдите величину угла AOB (в градусах).
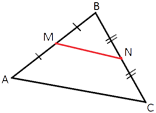Точки M и N являются серединами сторон AB и BC треугольника ABC, AC=42. Найдите MN.
В окружности с центром в точке О проведены диаметры AD и BC, угол ABO равен 75°. Найдите величину угла ODC.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: