Радиус окружности, описанной около квадрата, равен 48√2. Найдите радиус окружности, вписанной в этот квадрат.
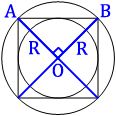Проведем диаметры
описанной окружности, как показано на первом рисунке.
Очевидно, что
квадрат разделился на 4 равных треугольника, углы, которые опираются на центр окружности (О), равны 360°/4=90°, т.е. эти треугольники
прямоугольные.
Тогда, по теореме Пифагора:
AB2=R2+R2
AB2=2R2
AB2=2(4√2)2
AB2=2*16*2=64
AB=√64=8
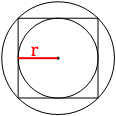Проведем радиус
вписанной окружности, как на втором рисунке.
Очевидно, что:
r=AB/2=8/2=4
Ответ: 4
Поделитесь решением
Присоединяйтесь к нам...
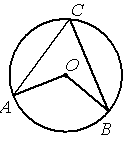Точка О – центр окружности, /AOB=110° (см. рисунок). Найдите величину угла ACB (в градусах).
Найдите тангенс угла С треугольника ABC, изображённого на рисунке.
В окружности с центром в точке О проведены диаметры AD и BC, угол
OCD равен 55°. Найдите величину угла OAB.
На отрезке AB выбрана точка C так, что AC=60 и BC=27. Построена окружность с центром A, проходящая через C. Найдите длину отрезка касательной, проведённой из точки B к этой окружности.
Радиус окружности с центром в точке O равен 29, длина хорды AB равна 40 (см. рисунок). Найдите расстояние от хорды AB до параллельной ей касательной k.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: