
 Сторона равностороннего треугольника равна 14√3. Найдите медиану этого треугольника.
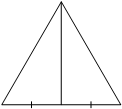
Сторона равностороннего треугольника равна 14√3. Найдите медиану этого треугольника.
 Введем обозначения как показано на рисунке.
Введем обозначения как показано на рисунке.
По
определению равностороннего треугольника:
AB=BC=AC=14√3
По
свойству равностороннего треугольника, медиана является так же и
биссектрисой, и
высотой.
Следовательно:
1) BD перпендикулярен AC (т.к. BD -
высота), т.е. треугольник ABD -
прямоугольный.
2) AD=AC/2 (т.к. AC - медиана).
По
теореме Пифагора:
AB2=BD2+AD2
AB2=BD2+(AC/2)2
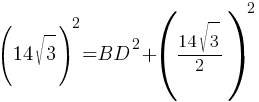
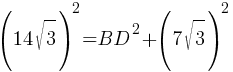
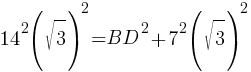
196*3=BD2+49*3
588=BD2+147
BD2=588-147=441
BD=√441=21
Ответ: 21
Поделитесь решением
Присоединяйтесь к нам...
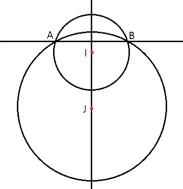 Окружности с центрами в точках I и J пересекаются в точках A и B, причём точки I и J лежат по одну сторону от прямой AB. Докажите, что AB⊥IJ.
Окружности с центрами в точках I и J пересекаются в точках A и B, причём точки I и J лежат по одну сторону от прямой AB. Докажите, что AB⊥IJ.
 ABCDEFGHIJ — правильный десятиугольник. Найдите угол CAH. Ответ дайте в градусах.
ABCDEFGHIJ — правильный десятиугольник. Найдите угол CAH. Ответ дайте в градусах.
 Лестница соединяет точки A и B и состоит из 20 ступеней. Высота каждой ступени равна 30 см, а длина – 40 см. Найдите расстояние между точками A и B (в метрах).
Лестница соединяет точки A и B и состоит из 20 ступеней. Высота каждой ступени равна 30 см, а длина – 40 см. Найдите расстояние между точками A и B (в метрах).
Какой угол (в градусах) описывает часовая стрелка за 2 минуты?
 В треугольнике со сторонами 2 и 4 проведены высоты к этим сторонам. Высота, проведённая к первой стороне, равна 2. Чему равна высота, проведённая ко второй стороне?
В треугольнике со сторонами 2 и 4 проведены высоты к этим сторонам. Высота, проведённая к первой стороне, равна 2. Чему равна высота, проведённая ко второй стороне?
Комментарии: