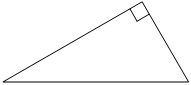
Один из острых углов прямоугольного треугольника равен 57°. Найдите его другой острый угол. Ответ дайте в градусах.
Обозначим неизвестный острый угол как α.
В
прямоугольном треугольнике один из углов прямой, т.е. равен 90°.
Тогда, по теореме о сумме углов треугольника:
180°=57°+90°+∠α
180°=147°+∠α
∠α=180°-147°
∠α=33°
Ответ: 33
Поделитесь решением
Присоединяйтесь к нам...
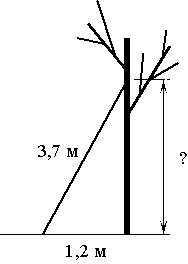Лестницу длиной 3,7 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 1,2 м?
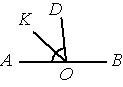Найдите величину угла DOK, если OK — биссектриса угла AOD, ∠DOB=108°. Ответ дайте в градусах.
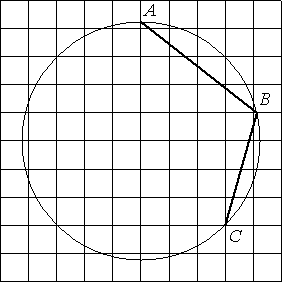Найдите угол ABC. Ответ дайте в градусах.
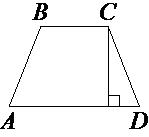Высота равнобедренной трапеции, проведённая из вершины C, делит основание AD на отрезки длиной 1 и 5. Найдите длину основания BC.
Пол комнаты, имеющей форму прямоугольника со сторонами 4 м и 10 м, требуется покрыть паркетом из прямоугольных дощечек со сторонами 5 см и 20 см. Сколько потребуется таких дощечек?
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: