Диагонали AC и BD трапеции ABCD с основаниями BC и AD пересекаются в точке O, BC=11, AD=15, AC=52. Найдите AO.
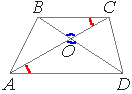Рассмотрим треугольники AOD и BOC.
По определению трапеции, AD||BC, а AC можно рассматривать как секущую при параллельных прямых. Тогда:
∠DAO=∠BCO (накрест лежащие углы).
∠AOD=∠BOC (вертикальные углы).
Тогда, по первому признаку подобия (по двум углам), данные треугольники подобны.
Следовательно, можем записать пропорцию:
AD/BC=AO/OC
15/11=AO/OC
15*OC=11*AO
При этом AO+OC=AC=52
OC=52-AO, подставляем это равенство в ранее полученную пропорцию:
15*(52-AO)=11*AO
780-15*AO=11*AO
780=15*AO+11*AO
780=26*AO
AO=780/26=30
Ответ: 30
Поделитесь решением
Присоединяйтесь к нам...
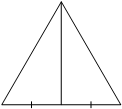Медиана равностороннего треугольника равна 13√3. Найдите его сторону.
Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=12, а расстояние от точки K до стороны AB равно 9.
В параллелограмме ABCD диагонали AC и BD пересекаются в точке O. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника COD.
В окружности с центром в точке О проведены диаметры AD и BC, угол ABO равен 75°. Найдите величину угла ODC.
В треугольнике ABC угол C равен 90°, BC=6, sinA=0,6. Найдите AB.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: