
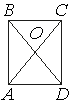
 Диагонали AC и BD прямоугольника ABCD пересекаются
в точке O, BO=37, AB=56. Найдите AC.
Диагонали AC и BD прямоугольника ABCD пересекаются
в точке O, BO=37, AB=56. Найдите AC.
BO=OD (по четвертому свойству прямоугольника).
Тогда:
BD=BO+OD=BO+BO=2*BO=2*37=74
AC=BD=74 (по второму свойству прямоугольника).
Ответ: 74
Поделитесь решением
Присоединяйтесь к нам...
 Четырёхугольник ABCD вписан в окружность. Прямые AB и CD пересекаются в точке K, BK=8, DK=12, BC=6. Найдите AD.
Четырёхугольник ABCD вписан в окружность. Прямые AB и CD пересекаются в точке K, BK=8, DK=12, BC=6. Найдите AD.
 Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 8.
Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 8.
 Из точки А проведены две касательные к окружности с центром в точке О. Найдите расстояние от точки А до точки О, если угол между касательными равен 60°, а радиус окружности равен 8.
Из точки А проведены две касательные к окружности с центром в точке О. Найдите расстояние от точки А до точки О, если угол между касательными равен 60°, а радиус окружности равен 8.
 В выпуклом четырёхугольнике NPQM диагональ NQ является биссектрисой угла PNM и пересекается с диагональю PM в точке S. Найдите NS, если известно, что около четырёхугольника NPQM можно описать окружность, PQ=86, SQ=43.
В выпуклом четырёхугольнике NPQM диагональ NQ является биссектрисой угла PNM и пересекается с диагональю PM в точке S. Найдите NS, если известно, что около четырёхугольника NPQM можно описать окружность, PQ=86, SQ=43.
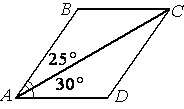 Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 25° и 30°. Найдите больший угол параллелограмма.
Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 25° и 30°. Найдите больший угол параллелограмма.
Комментарии:
(2021-10-18 13:11:07) Администратор: Никитина Тамара, Я не помогаю решить домашнее задание, цель сайта - подробно разобрать задачи, которые будут на экзаменах, чтобы учащиеся научились их решать самостоятельно. Если найдете похожую задачу на сайте fipi.ru, отправьте заявку на добавление задачи, и я ее обязательно добавлю.
(2021-02-23 08:28:10) Никитина Тамара: Диагонали осевого сечения усеченного конуса точкой пересечения делятся в отношении 2:1, считая от большего основания. Угол между диагоналями, обращенный к основаниям конуса, равен 60. Длина диагонали равна 3. Найти объем усеченного конуса.