
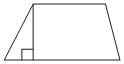
 Основания трапеции равны 5 и 13, а высота равна 9. Найдите площадь этой трапеции.
Основания трапеции равны 5 и 13, а высота равна 9. Найдите площадь этой трапеции.
По формуле площадь трапеции:
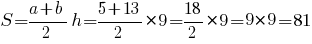
Ответ: 81
Поделитесь решением
Присоединяйтесь к нам...
 Один из углов ромба равен 114°. Найдите меньший угол этого ромба. Ответ дайте в градусах.
Один из углов ромба равен 114°. Найдите меньший угол этого ромба. Ответ дайте в градусах.
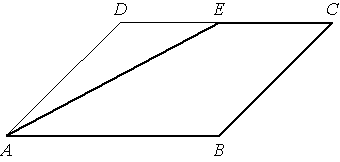 Площадь параллелограмма
ABCD равна 56. Точка E — середина стороны
CD. Найдите площадь трапеции AECB.
Площадь параллелограмма
ABCD равна 56. Точка E — середина стороны
CD. Найдите площадь трапеции AECB.
Укажите номера верных утверждений.
1) Медиана равнобедренного треугольника, проведённая из вершины, противолежащей основанию, перпендикулярна основанию.
2) Диагонали любого прямоугольника делят его на 4 равных треугольника.
3) Для точки, лежащей внутри круга, расстояние до центра круга меньше его радиуса.
 В трапеции ABCD боковая сторона AB перпендикулярна основанию BC. Окружность проходит через точки C и D и касается прямой AB в точке E. Найдите расстояние от точки E до прямой CD, если AD=14, BC=12.
В трапеции ABCD боковая сторона AB перпендикулярна основанию BC. Окружность проходит через точки C и D и касается прямой AB в точке E. Найдите расстояние от точки E до прямой CD, если AD=14, BC=12.
 Касательные в точках A и B к окружности с центром O пересекаются под углом 28°. Найдите угол ABO. Ответ дайте в градусах.
Касательные в точках A и B к окружности с центром O пересекаются под углом 28°. Найдите угол ABO. Ответ дайте в градусах.
Комментарии: