Установите соответствие между функциями и их графиками.
ФУНКЦИИ
А) y=-x2-5x-2
Б)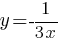 
В) 
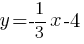
ГРАФИКИ
1) 
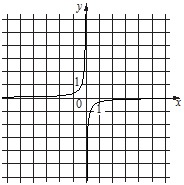2) 
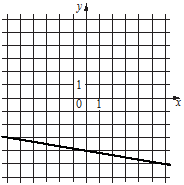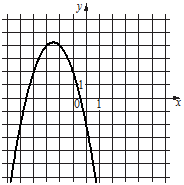
3) 
В таблице под каждой буквой укажите соответствующий номер.
Рассмотрим функции:
А) y=-x2-5x-2 - квадратичная функция. График любой квадратичной функции парабола. Т.е. подходит график 3).
Б) 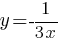- степенная функция (или обратно пропорциональная). Ее график гипербола. Т.е. подходит график 1).
В) 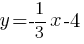- линейная функция - прямая. График 2).
Если вы сомневаетесь и хотите себя перепроверить, правильно ли вы определили соответствие, то можно поступить следующим способом (для примера проверим для функции -x2-5x-2):
1. Приравняем х, например, к нулю.
2. Подставляем 0 в функцию: y=-02-5*0-2=-2.
3. Проверяем, какому из предложенных графиков принадлежит точка (0;-2).
4. Очевидно, что подходит только график 3).
Если x=0 не очень удобное значение, возьмите любое другое, легкое для вычисления значения функции.
| ФУНКЦИИ | А) | Б) | В) |
| ГРАФИКИ | 3) | 1) | 2) |
Поделитесь решением
Присоединяйтесь к нам...
На рисунке изображены графики функций вида y=kx+b. Установите соответствие между знаками коэффициентов k и b и графиками функций.
| КОЭФФИЦИЕНТЫ | ГРАФИКИ | ||
|
А) k>0, b<0 Б) k>0, b>0 В) k<0, b>0 |
1)  |
2)  |
3)  |
Установите соответствие между графиками функций и формулами, которые их задают.
| ФОРМУЛЫ | ГРАФИКИ | ||
|
1) y=-2 2) y=x-2 3) y=-2x |
А)  |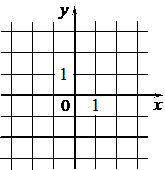
Б)  |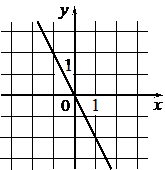
В)  |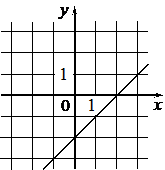
Постройте график функции
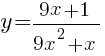
Определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
Известно, что графики функций y=x2+p и y=-2x-2 имеют ровно одну общую точку. Определите координаты этой точки. Постройте графики заданных функций в одной системе координат.
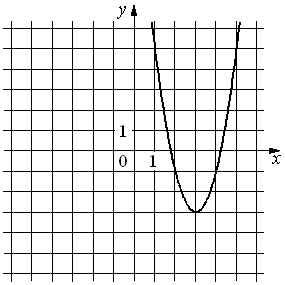На рисунке изображён график функции y=ax2+bx+c. Установите соответствие между утверждениями и промежутками, на которых эти утверждения удовлетворяются.
| УТВЕРЖДЕНИЯ | ПРОМЕЖУТКИ |
| А) Функция возрастает на промежутке Б) Функция убывает на промежутке |
1) [0; 2] 2) [2; 5] 3) [4; 7] 4) [1; 7] |
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: