Радиус окружности, вписанной в трапецию, равен 32. Найдите высоту этой трапеции.
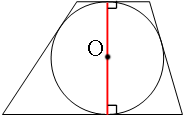Проведем радиусы к точкам касания с основаниями трапеции.
По первому свойству касательной (основания трапеции), она перпендикулярна радиусу.
Так как радиусы одновременно перпендикулярны параллельным основаниям трапеции, то получается, что радиусы представляют из себя единый отрезок или диаметр (это можно доказать если рассмотреть углы при параллельных прямых и секущей. Прямые углы являются односторонними и их сумма равна 180°).
Диаметр и является высотой трапеции:
h=D=2*R=2*32=64
Ответ: 64
Поделитесь решением
Присоединяйтесь к нам...
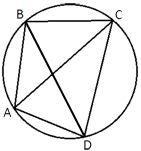Четырехугольник ABCD вписан в окружность. Угол ABC равен 92°, угол CAD равен 60°. Найдите угол ABD. Ответ дайте в градусах.
На стороне BC остроугольного треугольника ABC (AB≠AC) как на диаметре построена полуокружность, пересекающая высоту AD в точке M, AD=15, MD=3, H — точка пересечения высот треугольника ABC. Найдите AH.
В равнобедренной трапеции основания равны 3 и 7, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции.
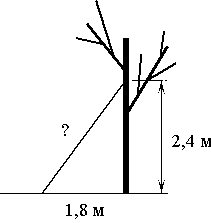Какова длина (в метрах) лестницы, которую прислонили к дереву, если верхний её конец находится на высоте 2,4 м над землёй, а нижний отстоит от ствола дерева на 1,8 м?
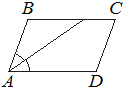Найдите острый угол параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 41°. Ответ дайте в градусах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: