Радиус окружности, вписанной в трапецию, равен 48. Найдите высоту этой трапеции.
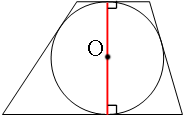Проведем радиусы к точкам касания с основаниями трапеции.
По первому свойству касательной (основания трапеции), она перпендикулярна радиусу.
Так как радиусы одновременно перпендикулярны параллельным основаниям трапеции, то получается, что радиусы представляют из себя единый отрезок или диаметр (это можно доказать если рассмотреть углы при параллельных прямых и секущей. Прямые углы являются односторонними и их сумма равна 180°).
Диаметр и является высотой трапеции:
h=D=2*R=2*48=96
Ответ: 96
Поделитесь решением
Присоединяйтесь к нам...
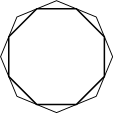Дан правильный восьмиугольник. Докажите, что если последовательно соединить отрезками середины его сторон, то получится правильный восьмиугольник.
Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 60° и 135°, а CD=36.
В параллелограмме ABCD диагонали AC и BD пересекаются в точке O. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника BOC.
На окружности отмечены точки A и B так, что меньшая дуга AB равна 66°. Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
Найдите площадь параллелограмма, изображённого на рисунке.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: