
 В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 25, 13 и 7. Найдите площадь параллелограмма ABCD.
В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 25, 13 и 7. Найдите площадь параллелограмма ABCD.
 По
свойству касательной:
По
свойству касательной:
OF - радиус окружности, т.к. OF проходит через центр окружности и перпендикулярен
касательной AC.
AG=AF
BG=BH=x
CH=CF=y
AF найдем по
теореме Пифагора:
AO2=AF2+OF2
252=AF2+72
625=AF2+49
AF2=576
AF=24=AG
EH -
высота параллелограмма. EH=OH+OE=7+13=20
SABC=p*r, где p - полупериметр, r - радиус вписанной окружности.
p=(AB+BC+AC)/2.
Рассмотрим треугольники ABC и CDA.
AD=BC и AB=CD (по
свойству параллелограмма).
AC - общая сторона.
Следовательно, по
третьему признаку равенства треугольников, данные треугольники равны.
Тогда:
SABCD=2*SABC
И в тоже время SABCD=EH*AD.
Приравняем полученные равенства:
p*r=EH*AD/2
(AB+BC+AC)/2*r=EH*BC/2
(AG+GB+BH+HC+CF+AF)*r=EH*(BH+HC)
(24+x+x+y+y+24)*7=20*(x+y)
(48+2x+2y)*7=20*(x+y)
336+7(2x+2y)=20*(x+y)
336+14(x+y)=20*(x+y)
336=6(x+y)
x+y=56=BC=AD
SABCD=EH*AD=20*56=1120
Ответ: SABCD=1120
Поделитесь решением
Присоединяйтесь к нам...
 Площадь прямоугольного треугольника равна 512√
Площадь прямоугольного треугольника равна 512√
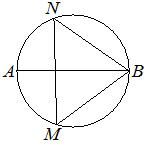 На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠NBA=36°. Найдите угол NMB. Ответ дайте в градусах.
На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠NBA=36°. Найдите угол NMB. Ответ дайте в градусах.
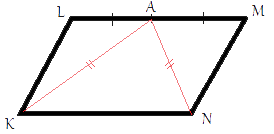 В параллелограмме KLMN точка A — середина стороны LM. Известно, что KA=NA. Докажите, что данный параллелограмм — прямоугольник.
В параллелограмме KLMN точка A — середина стороны LM. Известно, что KA=NA. Докажите, что данный параллелограмм — прямоугольник.
 Прямые m и n параллельны. Найдите ∠3, если ∠1=6°, ∠2=101°. Ответ дайте в градусах.
Прямые m и n параллельны. Найдите ∠3, если ∠1=6°, ∠2=101°. Ответ дайте в градусах.
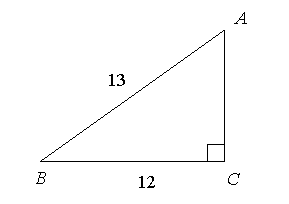 Найдите площадь треугольника, изображённого на рисунке.
Найдите площадь треугольника, изображённого на рисунке.

Комментарии: